S Parameters for PCB Simulation and Verification

By Deepak Kumar Behera , Sumit Varshney, Sunaina Srivastava, Swapnil Tiwari (Freescale)

Abstract

S parameters play a dominant role in high speed PCB simulation and verification. Generation of S parameters is relatively easy at high frequency in comparison to other parameters like Y and Z. In this article S parameter model, simulation of PCB parameters and measurements using VNA have been described. The measurements of PCB parasitic like inductance, capacitance, mutual inductance as well as mutual capacitance have also been discussed.

Printed Circuit Boards (PCBs) are extensively used in all the modern automotive, industrial, networking and communication systems. For a system working at sufficiently high speed a system designer must ensure that the point to point communication between any two points of the system is good in quality and integrity. A general system consists of single or multiple PCBs which have several connectors, passive components and simple to complex ICs. To ensure that the signal is transmitted from one end to other on the PCB without distortion, an advance analysis on signal integrity is required. This can help in understanding and characterizing the system for optimal performance.

At low frequencies simple voltage and current analysis can help us in analyzing and characterizing the system efficiently. But at high frequencies however, the wavelength of signals are comparable to or much smaller than the length of conductors. In this case, wave theory comes into picture and S parameters play a dominant role. For PCBs containing high speed DDRs, SERDES, PCI express etc die, package and board co-simulation methodology is adopted. For die and packages mostly, Spice or IBIS models are used and it is easy to use S parameters for the board. Modern signal integrity field simulators support the integrated analysis of Spice, IBIS and S parameter in a single simulation.

Generally the IC vendors and component manufacturers provide the SPICE or IBIS models which can be readily used in simulation environment but when we are designing the PCB we need to generate its simulation ready model locally. Generating a SPICE model becomes clumsy and sometimes the simulation may not even converge. Generation and use of S parameters is quite simple. Moreover for further analysis on parasitic like inductance and capacitance etc or any irregularities and discontinuities in the PCB S parameters can be easily converted to other parameters.

A typical PCB contains many components and traces. The traces can generally be classified as micro strip, strip lines or coplanar waveguides. Moreover there exist vias which should be effectively modeled. At sufficiently high frequency it is easy to measure signal properties in terms of transmission and reflection parameters rather than voltage, current, impedance and admittance etc. S parameters help us in treating the system as a black box and measuring its performance under any source or load conditions. We do not require an open or short test to generate these parameters as for Y, Z or H parameters. It is easier to measure the performance in terms of gain, loss and reflection coefficients and import the S parameter file in our advance SI simulation tools. S parameters can be easily cascaded and therefore we can fully characterize an interconnect path comprising of connector, cable and PCB traces.

S parameters can be defined for single port or multiple port system and are suitable for single ended as well as differential signal analysis. For all practical purpose generally the PCB traces are routed as controlled impedances. For a typical single ended configuration the control impedance is 50 Ω, for differential 100 Ω and for USB traces 90 Ω etc. Moreover as per requirements there exist other values as well. Applying a 50 Ω source or load termination and matching the impedance is quite easier. S parameters can help in generating as well as verifying high frequency models.

To have a quick glance at the S parameters let us consider PCB interconnect as two port network. Any PCB trace acts as a transmission line and may be single or differential in nature. Accordingly S parameters required for the traces could be single or differential in nature.

S parameters are defined as reflection and transmission coefficients. For a simple two port network as shown below in figure 1 the S parameters are defined as

B1 = S₁₁A1 + S₁₂A2 …………………. 1

B2 = S₂₁A1 + S₂₂A2 …………………. 2

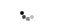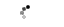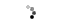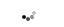
Figure 1: A two port network on PCB

The signal A1 which is incident on the PCB interconnect at port 1 is called the incident signal. Part of this signal is reflected as B1, and part of it is transmitted as B2 out of port 2. The ratio of the reflected signal, B1, to the incident signal, A1, is known as the reflection coefficient. The ratio of the transmitted signal, B2, to the incident signal, A1, is called the transmission coefficient. Similarly for signal A2 incident on port 2, B2 is the reflected signal and B1 is the transmitted signal.

For source and load matching the impedances in figure 1 have been shown as 50Ω assuming the PCB interconnect to be single and drawn on control impedance of 50Ω. Assuming the wave travelling from port 1 to port2 to be in forward direction, port 1 is assumed as input and port 2 as output, we can define the S parameters S11, S12, S21 and S22.

The reflection is a signal leaving port 1 as a result of a signal incident on port 1, and defines S11, the input reflection coefficient. The transmission is a signal leaving port 2 as a result of the signal incident on port 1 and defines S21, the forward transmission coefficient. Similarly S22 is the reverse reflection coefficient and S12 is the reverse transmission coefficient.

Similarly for differential signal PCB interconnects the S parameters can be defined as mixed mode S parameters. The differential channel or interconnect never remain purely differential due to asymmetry in length or width of traces or local dielectric constant hence the mixed mode S parameters come into picture. The details of mixed mode S parameter are beyond the scope of this article. Just to provide a brief insight the generalized mixed mode S parameters for a coupled interconnect are defined as below:

Bmc1 = S11Amc1 + S12Amc2 +S13Amd1 +S14Amd2

Bmc2 = S21Amc1 + S22Amc2 +S23Amd1 +S24Amd2

Bmd1 = S31Amc1 + S32Amc2 +S33Amd1 +S34Amd2

Bmd2 = S41Amc1 + S42Amc2 +S43Amd1 +S44Amd2

Where the subscripts 1, 2, 3, and 4 denote port 1, 2, 3, and 4 respectively. [S] Can be described by:

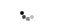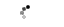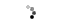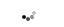
In the following we can call [Scom-com] the common s-parameters, [Sdiff-diff] the differential s – parameters and [Scom-diff] and [Sdiff-com] the mode – conversion or cross – mode s – parameters. In particular, [Scom-diff] describes the conversion of differential mode waves into common-mode waves, and [Sdiff-com] describes the conversion of common waves into differential waves.

While generating S parameters for the PCB traces we verify the stack up, identify the ports, provide source and load terminations and select the frequency range. Using good simulation tool S parameters are generated. For further analysis on capacitance and inductance S parameters are converted to Z or Y parameters. For analyzing the inductance offered by a trace if we convert S to Z then divide the imaginary part of Z by 2πf we get the inductance. For analyzing the capacitance similar process can be adopted by converting S to Z parameters. Sometimes during high speed analysis of PCBs or packages we want that the high impedance offered by the network should not fall in the desired frequency range. Every time we make modifications in the PCB or package design it might be difficult to directly generate Z or Y parameters at high frequencies. Therefore generating S parameters and then converting to other parameters and analyzing the board helps in quick analysis and correction of the design.

Once we receive the S parameters we can check and decide whether the file received is correct or not. Generally a PCB or a generic two port network comprising of connectors and traces is symmetric in nature. Therefore S11 and S22 must have same sign and value similarly S12 and S21 should correlate with each other. Before using the file containing S parameters in our simulation we should perform a visual check. If

|S₁₁|² +|S₁₂|²=1

Then the network is lossless and it can simplify the calculations required to extract the parameters. This relationship also holds well for low loss systems and at frequencies when skin effect resistance is very small.

Once the PCB has been designed and simulated we send it for manufacturing. After receiving the manufactured PCB with assembled components we perform several measurements to test and correlate the measured parameters with simulation results. A typical PCB consists of many connectors and a system consists of numerous PCBs. To fully characterize a system as already discussed we extract S parameters through measurements using VNA (Vector Network Analyzer) and feed this file as input into the field simulators.

PCB verification is carried out using TDR, TDT, and VNA etc. The TDR and TDT are used for time domain measurements and VNA is used to perform frequency domain measurements. At the desired frequency matching source and load impedances preferably 50 Ω is provided. The probes etc are chosen to align with the source and load impedance. The PCB acts as the DUT and its S parameters are measured at set power using a VNA. The VNA is calibrated before measurements are performed. The type of calibration depends on the frequency of operation.

VNA is used to perform one port or two port measurement depending on the requirements. To characterize connector, via and transmission lines on PCB one port measurement is performed. This helps in extracting inductance, capacitance and impedance as function of frequency by measuring the reflection coefficient S11 or S22. By opening and shorting the far end of a DUT we can find out the inductance and capacitance of the short structures on the PCB. To measure capacitance, the DUT should be left open ended and to measure inductance the far end of the DUT should be shorted to ground. Using Smith Chart the reflection coefficient is converted to normalized impedances and from there we obtain the inductance or capacitance.

For characterizing group of traces or interconnects and extracting their mutual capacitance and inductances two port S parameter measurements are performed. This involves the measurement of S12 and S21. The similar method of open and short structures on the DUT is used to measure the transmission coefficients S12 and S21. They are again converted to Z parameters and mutual inductance and capacitance is measured.

Moreover in cases where we cannot short or open the DUT we perform measurements using matched source and load terminations, extract the S parameters and directly use the model for use with other models to fully characterize a system as S parameters can be cascaded. Therefore S parameters prove to be a useful tool for PCB simulation and verification at high frequencies.

References:

1. Stephen H. Hall Garrett W. Hall James A. Hall “High Speed Digital System Design – A Handbook of Interconnect Theory and Design Practices”.

2. W. Fan*, Albert Lu, L. L. Wai, B. K. Lok, “Mixed-Mode S-Parameter Characterization of Differential Structures”

Authors:

Deepak Kumar Behera (deepak@freescale.com): Design Engineer with experience in signal integrity and package designing and analysis.

Sumit Varshney (b17255@freescale.com): Staff Design Engineer with expertise in physical integration, package designing and signal integrity

Sunaina Srivastava (b18098@freescale.com): Lead Design Engineer with experience in embedded systems, board designing and signal integrity.

Swapnil Tiwari (b36245@freescale.com): Design Engineer with experience in microwave antenna designing and signal integrity