


|
|

|
|
|
|
|||
|
How to cut power consumption for high-speed apps with A/D converter architecture
Continuous time delta-sigma (CTÄÓ) analog-to-digital conversion technology shatters the conventional wisdom that pipeline A/D converters are the only conversion technique available for high-speed, high dynamic range applications. CTÄÓ technology offers lower power operation, better dynamic performance, economy of design and specific functional benefits.
In short, CTΔ∑ technology means: 1. An inherently power-efficient architecture that eliminates power-hungry sample-and-hold amplifiers (SHA) and the wide-bandwidth gain stages essential to the pipeline A/D converter concept. CTΔ∑ architecture supports high-resolution analog-to-digital conversion systems from 10 to 16-bit and beyond with sampling rates up to 100 MHz. Today, most A/D converter design work aims to reduce power, particularly in high-speed conversion, and to minimize the number of comparators needed. It is broadly assumed that the pipeline converter provides the highest sample rates whilst yielding high dynamic range. It is used as a standard in data conversion applications at 10-bit and higher resolutions and for sample rates from 5 MHz to 100 MHz or more. The architecture reduces the number of comparators needed by deploying multiple low-resolution flash conversion stages cascaded together to form the pipe. Although the resolution of each conversion stage is reduced, saving on comparators, the first stage must be designed with linearity at least as good as the maximum resolution of the A/D converter (12-bit linearity for a 12-bit A/D converter). Different pipeline implementations exist, but all work by reducing a multi-bit conversion into several lower resolution “flashes” that are processed synchronously. At each stage in the pipe, a reconstruction of the previous stage’s quantized output, generated by a D/A converter, is subtracted from the original input signal. The residual signal is then amplified prior to moving onto the following stage for finer quantization. In pipeline conversion a sample-and-hold amplifier (SHA) is need to acquire the input signal and hold it to better than 0.5 LSB for the duration of the conversion. Once all sub-stages have a valid conversion result, a digital correction block constructs the final multi-bit result. The pipeline A/D converter is capable of high dynamic performance. However, beyond 12-bits resolution, as the sampled signal moves through the pipeline, transferring the charge associated with a given signal demands high gain bandwidth to ensure stage settling times fall within the limits set by the high frequency signals that are being sampled. To maintain linearity you need to calibrate and correct for the limits in component matching achievable with current process technologies and it is tough to migrate designs from one process to another. As operating voltages fall from one process generation to the next, the input signal headroom is compressed. Furthermore, designing switches with greatly reduced threshold voltages that work well in deep sub-micron processes gets harder. It’s worth remembering that pipeline A/D converters form only part of a data conversion system, you need in addition to find a low jitter clock source and design input stages that include anti-alias filters. In anti-alias filter (AAF) design, steep attenuation characteristics are hard to achieve, tempting you to consider over-sampling the signal of interest. Over-sampling stretches the Nyquist zone, lowering demands on filter roll-off but the trade-offs are increased system power and higher processing speeds demanded of the back-end DSP system. With continuous time delta-sigma conversion, on the other hand, you don’t need an AAF. Historical delta-sigma conversionThe Δ∑ converter uses a low-resolution quantizer - often only 1-bit - clocked at rates considerably greater than Nyquist demands. The quantizer creates a large number of low-resolution samples that, averaged over time, yield an increased dynamic range. The analog design is potentially straightforward, given the linearity of a 1-bit (2 level) quantizer. In the digital domain, filtering and decimation are needed to reconstruct output data and remove out-of-band noise. Figure 1 shows the simplest single order Δ∑ modulator block. It comprises a summing node, integrator and comparator. The comparator’s output feeds a 1-bit DAC that closes the modulator’s feedback loop. The modulator compares the input signal against a voltage reference level fed back from the DAC. The comparator is clocked at the over-sampling frequency. Assuming enough loop gain, the modulator is a pulse stream, the density of ‘1s’ or ‘0s’ of which is a direct digital representation of the input signal. The DAC switches between Vref to close the control loop.  Figure 1 Simplest single order Δ∑ modulator block Quantization errors within the modulator limit dynamic range. For the Δ∑ A/D converter, resolution increases are gained by balancing the over-sampling ratio, Δ∑ modulator order, and quantizer resolution. Over-sampling allows sample frequency/SNR trade-off and improves dynamic range (DR). It gives an SNR improvement of 6 dB (or 1-bit’s worth) for every quadrupling of the sample rate but DR is more effectively increased by increasing the resolution of the quantizer and/or by adding more integration stages to the modulator. Noise shaping is a property of Δ∑ A/D converters resulting from the application of feedback that extends dynamic range. This feature is best illustrated by the mathematical analysis of the feedback control loop of the Δ∑ modulator as modeled in the frequency domain, illustrated in Figure 2. 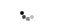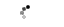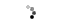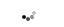 Figure 2 Noise shaping of Delta Sigma modulator This model reveals the key value of the Δ∑ modulator. A closed loop modulator works as a high-pass filter to quantization noise and as a low-pass filter to the input signal. The effect of this is a further increase in dynamic range of 9 dB for each doubling of the sample rate. Additional integrators within the loop can increase the steepness of the noise characteristic to give you further dynamic range increases. Figure 3 shows simulation results for the noise power density for the Δ∑ modulator used in a CTΔ∑ A/D converter. This FFT plot (with 65k points) of the modulator illustrates the noise power density (per FFT bin) relative to the input signal frequency. The simulation was driven with an input signal frequency of approximately 4.8 MHz. The minimum noise power density achieved by this modulator is 166 dBc/Hz (in the pass band). Note the characteristic of the out of band noise i.e. those frequencies above 20 MHz. Here noise power levels rise at the rate of 21 dB/octave, a tell-tale sign of a third order modulator. Deployed within this A/D converter design is a 16 levels, or 4-bit, quantizer that delivers 14-bit dynamic range at modest over-sampling rates. Having established a modulator system capable of achieving these low noise levels, the next stage is to apply filtering to eliminate out-of-band noise, and decimation to re-sample the data.  Figure 3 Noise over power density simulation results A digital filter must reject all signal components within the serial data stream that occur beyond the Nyquist bandwidth. Simplistically, two frequency selective filter structures can be implemented in the digital domain. They are the finite and infinite impulse response filter systems (FIR and IIR). FIRs are more widely used because they are simpler and have a linear phase response. IIR filter design is more complicated by virtue of the feedback included. The potentially infinite response of the IIR filter means there is always a possibility for the filter to become unstable. In addition, group delay can become significant and have adverse effects on performance in some systems. Many degrees of freedom exist for optimization of the signal transfer function in a CTΔ∑ A/D converter through combining different filter algorithms, however optimal solutions may require many cascaded stages of FIR and IIR sections. Digital filtering allows for the data reduction or down-sampling necessary to provide output data at the originally intended sample rate. Note that over-sampling provides large amounts of redundant data. The process of sample rate reduction is called decimation. In summary, these are the basic elements of a delta-sigma A/D converter. Firstly, over-sampling spreads quantization noise. Secondly, noise shaping reduces the in-band noise at the expense of higher out-of-band noise. Thirdly, digital filtering attenuates out-of-band noise and signal components. Continuous time versus discrete time systems Pipeline and DTΔ∑ A/D converters have a common design thread. In discrete time, sampling an input signal requires that the signal be acquired at a precise moment in time. For an accurate representation of the input signal to be acquired on a hold capacitor, it is necessary that the input stages settle to a finite level, dictated by the accuracy limits of the system, in a time period driven by the system sample rate needs. This settling time eats into the sample time period of the system. At 40 MS/s a conversion system will have a sample period of just 25 ns, which sets the maximum time limits for circuit settling. At higher resolutions this drives a need for very high gain bandwidth circuits within the acquisition signal path. In fact, the converter system must be designed with circuits that work with bandwidths many times that of the input signal. Discrete time circuits therefore have to burn excess power to process a given bandwidth. The move to a continuous time strategy eliminates the settling time issue altogether, allowing either a lower power CTΔ∑ A/D converter implementation, versus discrete time, at a given sample rate or a higher sample rate for a given power budget. The continuous time implementation With CTΔ∑ the filter performance is dependent on conventional active filter design rules. If the sample rate is changed to match input signal bandwidth the CT filter must be tuned. Therefore, a potential limit on the CTΔ∑ implementation is how to ensure that a wide range of sample rates can be supported from a single product platform. This problem is solved using adaptive filter networks in combination with calibration techniques. For high-resolution implementations the loop filter must have significant gain to obtain high linearity. This is provided using multi-path and cascaded gain stages operating at 1.2 V and delivering 80 dB of gain for a 30 MHz bandwidth. This has been clearly demonstrated as possible in 0.13 ìm CMOS. The first product to implement CTΔ∑ conversion offers a low power alternative to the pipeline converter. It is said to be a complete data conversion system, designed to operate seamlessly over a wide range of sample rates without high-performance, expensive, external components. Highlights of this architecture include: Advantages of CTΔ∑ implementation Power consumption some 50% lower than the best existing pipeline designs Inherent anti-alias filtering simplifies the A/D converter input circuit  Figure 4 CT Δ∑ A/D converter eliminates complex input filtering High dynamic range and low over-sampling rates Xignal uses a third-order CTΔ∑ modulator, designed around a 4-bits quantizer stage helping it to achieve considerable dynamic range at an over-sampling rate of 16. The differential input signal path has a bandwidth of 30 MHz. The internal sample clock operates at 640 MHz. The base technology today allows for increased sample rates to 80 MSPS (at 14-bits) with an over-sampling clock rate of approximately 1.3 GHz. Through self-adaptive tunable loop filter components the A/D converter is optimized for sample rates from 20 to 40 MSPS. A low jitter PLL provides an accurate sample clock Alternatively, an external clock can drive the A/D converter. High frequency jitter from an external distributed clock tree will be removed provided its jitter falls outside the 350 kHz PLL bandwidth of the jitter cleaner circuit. However, a further advantage of the on-chip precision clock is that it can be routed to external circuits and used as a system reference clock for other time-critical parts of the system, potentially eliminating the extra cost of a low jitter source, saving both design effort and board area. A low jitter clock is a crucial function in all high-speed, high-resolution data conversion systems. Phase accuracy of the sample clock has a major impact on measured performance. In fact, decibels of dynamic range are easily sacrificed by picoseconds of phase jitter. Figure 5 shows the mathematical derivation of maximal clock jitter for a given resolution and input signal frequency. For a 10 MHz bandwidth signal, at 12-bit resolution, clock jitter must be less than 3 ps RMS. For 14-bits, this demand drops to 1 ps RMS. 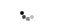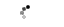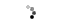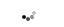 Figure 5 Maximal clock jitter Summary The quantization noise simulation result illustrated by Figure 3 hints at the unrealized dynamic range of a multi-bit Δ∑ modulator. There is some room for further dynamic range improvements with careful design, particular with respect to thermal noise, the dominant noise source in this design today. The ongoing development at Xignal shows that the A/D converter core can be successfully combined with input signal path components to provide a high level of integration. The digital processing (filtering and decimation) provided also shows that in future it is possible for system designers to tailor transfer functions for a given application. Finally, the elimination of external anti-alias networks and the inclusion of a high performance PLL significantly ease the design of a high-resolution high-speed sampling system. Though complex, the technology deployed CTΔ∑ A/D converter has been implemented in such a way to be transparent to the user, making this one of the most complete and easiest-to-use data acquisition systems available. Its implementation challenges some of the key assumptions made by designers developing high performance data conversion systems and offers a unique alternative. About the authorMark Holdaway is the director of product marketing for analog to digital converters at Xignal Technologies GmbH. You can contact him at mark.holdaway@xignal.de |
|||
|
|
|
|
|
Home | Feedback | Register | Site Map |
|
|
|
All material on this site Copyright © 2017 Design And Reuse S.A. All rights reserved. |