Placement of different type nodes in a Network-on-chip graph

By Yuriy Sheynin., Elena Suvorova,
St. Petersburg University of Aerospace Instrumentation.
St. Petersburg, Russia
   
Abstract:

In this article we consider effect of different type nodes placement in a network-on-chip to system parameters. We suggest a method of nodes placement that guarantee the potential performance constraints meeting. In general case the placement task is NP-complete. Suggested method allow essentially decrease the algorithm complexity. This method can be used for wide class of networks-on-chip.

Introduction

Modern network-on-chip could include different types of nodes. Generally nodes that are of-chip external interconnections controllers – external nodes, are used in the system for I/O. Internal nodes could also be divided to some groups according to their specific functions

For these systems the node placement into interconnection graph becomes very important. In respect to a set of system tasks and node's parameters we could determine average or maximal allowed transmission time between nodes of different types. The placement of nodes in interconnection graph must allow the system to meet that average or maximal time constraint.

The placement of nodes different types in interconnection graph determines the number and the length of paths between nodes. The average data transmission time depends on parameters that are determined by the interconnection graph; it also depends on throughput and load of channels between nodes. Throughput of channels is determined by its physical and logical organization (data transfer protocol). The load of data channels in one time moment is determined by tasks that are running in system and their mapping to nodes. Also load of data channels depends on the path selection method between destination and source nodes. In this article we suggest that for message transfer shortest path is used. If more than one shortest path exists then the path selected occasionally or the path is selected on base of information about system load.

Modern interconnection system for networks-on-chip can be switch based or based on direct interconnections between nodes

In a network-on-chip based on direct links between nodes every node corresponds to a vertice in the interconnection graph. For switch based network every node and every switch corresponds to a vertice in the interconnection graph

We suppose here that all tasks in the system send messages with the same average length. In this case average message transmission time could be determined as:

T_s=(D_s-1)× T_o + D_s× T_r;    (1)

In these formula:

• T_s  – average message transmission time;
• D_s – the number of message transmissions between nodes;
• T_o – the average time that message stayed in transit node (includes waiting in queue)
• T_r  – the average time of transmission message between nodes.

For system tasks we could form a rate of messages flows between nodes of different type’s matrix L. The value of element Lij of this matrix is equal to the message flow rate between nodes of type i and type j. Let’s consider that a node of type i will send messages to nearest node of type j. If some nodes belong to the type j lied at the same distance from the node i then the message flow will be uniformly distributed between these nodes.

Let’s consider that all messages have equal priority, same average time of processing in transit nodes and are placed in common queue (FIFO) in a transit node.Then the average load of a node could be determined as:



where:

• R – the average node load;
• T – the average time of message processing in a transit node;
• Lij – the message flows rates that are going through this node;

The average time that message stayed in queue of one transit node:



where W – the average time that message stayed in queue.

The average time that message stayed in a transit node:



Let’s consider how affect the node placement to message transmission time by the example of 2D-grid includes 16 nodes. This system includes three external nodes and four special nodes. In figure 1 two variants of placement is presented.



Figure 1. The variants of node placement

The black positions on this figure corresponds to external nodes, the chequered positions corresponds to special nodes, the direct lines show interconnections between nodes, the arches show message ways to and from external nodes, the dotted arches show message ways to and from special nodes. On figure 1,b the nodes placement provides minimal distances to nodes of all types and minimal deviation number of nodes connected to nodes of every type from average (node connection deviation) reachable for this topology. Let’s consider how strong the message transmission time depends on node placement. The graphics on figure 2 shows correlation between average message transmission time and message rate (l1 – rate to/from external nodes, l2 – rate to/from special nodes, T11 – transmission time to/from external nodes, T12 – transmission time to/from special nodes for placement presented on figure 1,a; T21, T22 – similar times for placement presented on figure 1,b). The average message transmission time for placement presented on figure 1,b practically not depended on message rate but for placement presented on figure 1,a this time grows in tens times  (for message rates less than message processing rates)



Figure 2. Dependency between average message transmission time and message rate

Accordingly with this the nodes of different types must be placed in interconnection graph in such a way that for given values of parameters T and Tr the average message transmission time was not more than a given value of Ts.  On level of interconnection graph the distance to  nodes of viewed type and the node connection deviation must be less than appropriate constraints (the average time that message waits processing in node of viewed type essentially depends from the second parameter).

In general case the message transmission time between nodes of two viewed types depends on propagation of other types messages in system. Therefore detail evaluation of message transmission time could be made only after placement of all nodes. The placement task is NP-complete. For its decision in case of tens nodes and more than two types need a lot of computation resources.

In this article we suggest the method that allow to decrease the placement complexity. It could be used for wide class of systems.

If nodes message rate between that is high are placed closely then the average placement time reduced because small number of transit nodes on message way. Also if message way will be shorter, through every transit node will goes less messages. As a result queue length in transit nodes will be shorter and waiting in queue time will decrease.

Transmission time between nodes of two selected types depends on propagation of messages between nodes of other types. As result in case when user not defined strong timing constraints for messages goes between two selected node types but message rate is high the minimization of distance between these node types is need. It allows minimize number of transit nodes in way of these messages and load of whole communication system. As result transmission time for other types of messages that goes through same transit nodes will be smaller.

The placement algorithms, the weighted p-median algorithm

In previous work we consider possibility of placement nodes of two types, for example external nodes and computing nodes, in interconnection graph [1]. For decision of this problem we suggest the algorithm based on classical algorithm for graph p-median determination [2,3] (hereinafter the weighted p-median). This algorithm could not be used for placement more than two types of nodes because its complexity extremely grows. As distinct from classical algorithm for graph p-median determination our algorithm allows to distribution of message flow from node (vertice) with type i to some nodes with type j if all these nodes are placed at the same distance (and shortest) from node i. This is important for reflection of a networks-on-chip specific. This algorithm was used for placement 3 external nodes in network-on-chip graph based on 2-D torus that includes 20 nodes. As result the average transmission time from internal node to external node decreases in 1.5 times (average transmission time between internal nodes not changed)

This algorithm could be used as ground of algorithm for placement of some node types: the weighted p-median could be processed for every node type and after that between selected for every type node sets could be found not crossed sets. This algorithm allows found all existing decisions that meet user constraints.

The complexity of algorithm based on graph p-median determination essentially grows with the number of nodes and with number of node types. For example determination of p-median that includes 5 nodes is in 15 times more complex than determination of p-median includes 3 nodes for 2D-grig includes 36 nodes.

Also for some node types the complexity of algorithm grows proportional the number of types. In first time the weighted p-median algorithm is repeated for every type, then the complexity of final sets selection depends on number of types. As result this algorithm could not be used directly for systems that include hundreds of nodes and tens of node types.

The methods for complexity decreasing – Graph Division

For complexity decreasing the initial graph could be divided into subgraphs. Then for every subgraph the weighted p-median algorithm could be used. This method allows strongly decrease complexity on p-median selection stage. But not all decisions that meet user constraints will be found. With the subgraph number growing the number of lost decisions growing also. The number of lost decisions depends not only on number of subgrahps but also on division algorithm.

This problem is illustrated by example showed on figure 3. The graph includes 16 nodes. Let’s select median that includes 4 nodes with max distance equal one and max deviation equal 0. For this graph exists two p-medians that meet this constrains, they are represented on figure 3 a,b (selected vertices are black). If the graph is divided on two subgraphs as shown in figure 3 c, only one decision could be found. If the graph is divided as shown in figure 3d, decisions could not be found.



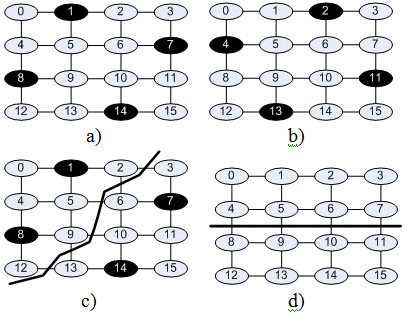
Figure 3. Weighted p-median selection in initial and divided graph

If subgraphs include tens nodes then the number of lost decisions strongly decreases, but results are little worst than for selection in whole graph. Also most of topologies that used for NoC are regular or practically regular. For them typically some symmetrical weighted p-median exists. If some of these medians are lost others compensate this. (In example represented in figure 3 a, b p-medians are symmetrical.)

Now exist a lot of graph division algorithms. For most of them the main criterion of division quality is minimization or maximization of summary number (or summary weight) of dissected edges. For graph division could be used geometrical and combinatorial methods. Geometrical method are simple but the division quality in many cases is worse than for combinatorial methods [4,5,6,7].

But for our task the criterions that used in these algorithms is not employed. For our task the optimal graph division is division in which all vertices that connected to the median vertice are in same subgraph. If they are in different subgraphs then the p-medians that selected in subgraph are displaced in comparison with p-medians that selected in initial graph. The direct dependency between number of dissected edges and division quality don’t exist.

Because of that we suggest others criterions: the minimization of diameter and average diameter of subgraphs. Also every subgraph must be connected.

In difference from the considered before methods, in what the graph could be divided into subgraphs includes not equal number of vertices, for our task we recommend division to subgraphs with equal number of vertices. In every subgrapsh the equal number of p-median vertices is selected.

For graph division we are using the wave algorithm [8]. The vertice with minimal valence is selected as the wave source. It includes in first subgraph. Then in this subgraph includes vertices that lays on distance 1 from the selected vertice, after that the vertices lies on distance 2 and so on until this subgraph will include given number of vertices (equal the vertices in initial graph number and the subgraph number ratio). When next vertice selected the remained part of initial graph must be connected graph. The vertice not included in the subgraph if this condition is violated. Because of this condition we can divide the remained part of graph into connected subgraphs.

After first subgraph is composed in remain part of initial graph again selected vertice with minimal valence and next subgraph found. This algorithm repeated until all subgraphs are composed.

If system includes some types of vertices for every of them the initial graph could be divided on different number of subgraph in compliance with number of vertices in the type. If the number of vertices in some types is equal we also use different graph divisions to minimize the effect of lost decisions.

This algorithm was used for placement of vertices in 2D-grids, 3D-grids, torus based on 2D-gris and 3D-grid, hypercube with number of vertices 16 - 128. The number of vertices in one type is 4 – 12. The initial graph in divided into 2 – 4 subgraphs. For analysis the maximal reachable constraints are used (the minimal value of maximal distance to p-medians, the minimal value of node connection deviation). The maximal distances that are received for divided graph is in 1,01 – 1,5 times bigger, the average distances are practically equal, the node connection deviations are in 1,1 – 1,25 times bigger than received for initial graph. When the number of vertices increases the receiving results will be better. The complexity is decreased in 10 – 15 times for divided graph. As long as for many tasks users needs parameters on 10 – 20% less strict than maximal reachable, using of the division algorithm is acceptable.

The methods for complexity decreasing – parallel placement

The division of initial graph into subgraphs allows decreasing of selection weighted p-median complexity. But if many node types exist in system and for every type a big number of p-medians selected then the complexity of selection non crossed variants also could be not acceptable large.

Let’s consider that 3 node types exists in the system and the number of nodes of every type is equal. For node placement we need to use the weighted p-median algorithm two times, for example for placement nodes of first and second types (in this case the nodes of third type will be placed automatically on free points). Among selected variants will be many equivalent (or very closed) by its parameters and practically equivalent variants. This situation illustrated by figure 4. On this figure the nodes of one type are equally colored. The variant represented on figure 4 a, b are equal (the maximal distance, the average distance and the node connection deviation for these variants are equal) and variant 4c lightly differ (the difference between the maximal distance, the average distance and the node connection deviation for these variants less than 5%).



Figure 4. weighted p-median selection variants

If system includes some tens of nodes the number of equal and practically equal variant will be very large and complexity of weighted p-median algorithm will be too big.

To decrease the complexity we suggest the algorithm of parallel placement of all node types in interconnection graph. It oriented to uniform proportional placement the nodes of all types in graph. Let the rate of number of nodes of type I in system and whole number of nodes is xi. If we view random node in the graph and select the subgraph with center in this node and arbitrary diameter then for this subgraph the rate of number of type I nodes and whole number of nodes tend to xi with increasing of the subgraph diameter. The ground condition of this algorithm is essentially less strict then the ground conditions of weighted p-median algorithm. This allow essentially decrease the complexity of node placement algorithm.

Let’s determine the field of this algorithm application. If the maximal distance until the nodes of viewed type essentially less than diameter of graph (in this case the number of nodes of this type will be big, else the placement is not possible), then using of parallel placement algorithm is appropriate (in this case the weighted p-median algorithm gives a lot of equal variants)/ Also this algorithm could be used if user define not strong constraints for maximal distance and node connection deviation.

We suggest two variant of the parallel placement algorithm realization. The first variant has minimal complexity but the second variant allows receiving better system parameters. In first placement variant the first node randomly selected (as show experiments with different topologies the results weakly dependent from first node selection). Then the nodes selected consequently with using of wave algorithm (at first the nodes lies on distance one from started node selected, then the nodes lies on distance 2 and so on). For every node determines its type. For this determines the rate of placed nodes to whole number of nodes for every node type and selected type with smallest rate.

In second variant of parallel placement algorithm at the start point for node numbers of all types is derived the greatest common divisor. After that derived the adjusted numbers of nodes for every type and sum of these adjusted values - Sr. Then randomly selected the first node (as for first variant). With using of wave algorithm selected subgraph with center in this node and includes Sr nodes (let’s designate it closed subgraph). For every node in this subgraph determines its type (as in first variant). After that selected the node in witch closed subgraph exists nodes with not defined type. If in initial graph some nodes meet this constraint selected the node in witch closed subgraph is the least number of nodes with undefined type. For nodes with undefined type in selected subgraph determines its type. This process repeat until the graph includes nodes with undefined type.

The results received with using of parallel placement algorithm (variant 1 and 2) and weighted p-median algorithm for 2D-grids with different number of nodes and different number of node types represented on figure 5. The average distance to all node types (the average value of average distances from all nodes to every node type) for all these algorithms is practically equal. The maximal distance and the node connection deviation for first variant of parallel placement algorithm is in 1,5 – 2 times worst, for second variant is in 1,2 – 1,4 times worst than for weighted p-median algorithm. But the complexity of weighted p-median algorithm is in 10 – 100 times bigger.
 



Figure 5. The maximal distance, the average distance and the node connection deviation for different placement algorithms

The complex method for node placement

We suggest using the combination of weighted p-median algorithm and parallel placement algorithm for complex systems that includes big number of node types and different constraints to placement nodes of different types.

In this case we suggest selection of node types for what strong constraints to placement exist (maximal distance to nodes of this type and the node connection deviation). For these node types we recommend using of the weighted p-median placement algorithm. Then for other node types could be used parallel placement algorithm (for placement of these nodes are used the positions, that remain free after the first group of nodes placed). This combination allows reaching got system parameters with acceptable complexity.

References

1. Suvorova E. A., Sheynin Y. E. The interconnection graphs and node placement for NoC. MES-2005 pp. 387-393 (in Russian)

2. Hararry F. The graph theory. M. Mir, 1973. 300 p. (in Russian)

3. Kristofides N. The graph theory: algorithmic approach. M, Mir 1978. 432 p. (in Russian)

4. Berger M., Bokhari S Partitioning strategy for nonuniform problems on multiprocessors IEEE Transactions on Computers. 1987. C-36(5). P. 570–580

5. Heath M., Raghavan P A Cartesian parallel nested dissection algorithm SIAM Journal of Matrix Analysis and Applications, 1995. 16(1). P. 235-253

6. George A., Liu JComputer Solution of Large Sparse Positive Definite Systems Prentice-Hall, Englewood Cliffs NJ, 1981

7. Schloegel K., Karypis G., Kumar V Graph Partitioning for High Performance Scientific Simulations 2000

8. B. W. Kernighan and S. Lin, An efficient heuristic procedure for partitioning graphs, Bell System Tech. J., 49 (1970), pp. 291-307