Pipeline AES S-box Implementation Starting with Substitution Table

Valeri Tomashau, LC Engineers, Inc.
Rahway, NJ, USA

Abstract :

The SubByte transformation, carried out by S-box, is the most time consuming procedure in Advanced Encryption Standard (AES) algorithm. A look-up table is commonly used for SubByte transformation in AES implementations on FPGAs. Since the S-box is on a critical path, the delay contributing by the 256-byte look-up table constrains the maximum operating frequency of AES processor and hence its throughput. In an effort to increase the throughput via pipelining it is proposed to decompose the initial 256-byte look-up-table into the set of smaller multiplexer-switched look-up tables. Suggested approach applies both to FPGA and to ASIC look-up-table based AES implementations.

INTRODUCTION

The Rijndael cryptographic algorithm, proposed by Joan Daemen and Vincent Rijmen, has been adopted as a standard (AES) by the US National Institute of Standards and Technology (NIST) in 2001 [1].

This paper is focusing on the most time consuming step of the AES algorithm. This step is a Non-Linear Byte Substitution that transforms some byte value into a new byte value through the use of an S-box Substitution Table [2]. This table contains pre-computed inverted values for each of the 256 8-bit numbers (bytes) considered as elements of the Galois finite field GF(2⁸).

There are two essentially different and widespread methods of S-box hardware implementation. One of these methods consists in immediate using of S-box substitution table, stored in a Look-Up Table (LUT). The S-box of this type is fast, however, it is expensive in terms of hardware.

Another method is based on the calculation of the S box functions using composite field arithmetic operations. Thus, finding an inverse in GF(2⁸) is reduced to an inverse in more simple GF(2⁴) and additional multiplications. The method goes back to Rijmen's suggestion [3]. Such reduction enables relatively simple hardware implementation of the S-box. Although the S-box implementation of this type is significantly smaller than the LUT-based implementation by area and has the capability to be pipelined, it is more time and energy consuming.

There are some immediate ASIC-implementations of S-box logic functions [4, 5]. They are close to LUT-based straightforward implementations by delay and can be pipelined.

A. Hodjat and I. Verbauwhede [6] have performed a comparison by area and time between non-pipelined LUT-based S-box implementation and three S-box implementations based on composite field: non-pipelined (single stage), 2 stage pipelined, and 3-stage pipelined. They have found that the non-pipelined LUT-based implementation is fast (in terms of throughput) as 3-stage pipeline composite field implementation. However the last one is 23% smaller in area. In addition, the authors of [7] stated that the LUT-based S-box "cannot be pipelined". In contrast to the above statement, the method suggested in this paper allows pipeline implementation of AES S-box without losing the advantage of the LUT-based approach.

Since LUT-based S-box is fast acting, it would be reasonable to apply the LUT-based approach to S-box hardware implementation as the starting point for its further improvement through pipelining. Whenever a higher AES processor throughput outweighs the area limitations, suggested method is beneficial.

Although the LUT-based S-box cannot be pipelined as such, the associated circuit being explicitly implemented can be pipelined. Another way to obtain the pipelined LUT-based S-box is to break down the initial 256-byte look-up-table into the set of smaller look-up tables. Initially, these tables are used to get intermediate results while the final result is selected among them by multiplexing.

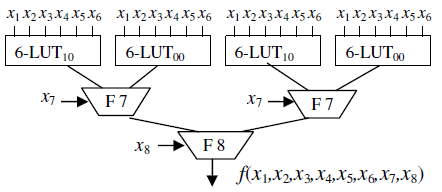
Fig.1. Non-pipeline Xilinx Virtex-5 implementation of an arbitrary 8-variable logic function (four 6- LUTs are required)

I. DECOMPOSITION OF S-BOX FUNCTION AND ITS NON-PIPELINE FPGA IMPLEMENTATION

Let us take a look at the S-box as a set of eight logic functions of eight variables. The Sum-of-Products (SOP) representation for these functions may be easily derived from the S-box substitution table that is nothing but the truth table for the set of these functions. Since the simultaneous optimization of the set of the S-box logic functions is not a subject of this paper, the sole 8-variable function will be under further consideration. This function can be defined by 256-bit look-up table, or 256 bit string, or a string of 32 HEX digits.

The Goal of multilevel implementation of an 8 variable logic function is to allow for its pipelining. Let us represent the initial function in the form of superposition of simpler logic functions. The suggested technique is limited by well-known Shannon expansion as universal means for the decomposition of an arbitrary logic function in the form of SOP.

Specifically, Xilinx Virtex-5 FPGA [7] is taken as target hardware. The 6-input function generator is the basic element of this FPGA. Each 6-input function generator is programmable as a 6-input Look-Up Table (6-LUT) to implement any logic function of six variables.

Four 6-LUTs along with built-in multiplexers F7, F8, and a configurable register form a slice. When configured properly with the use of the internal multiplexers F7 and F8, a single Virtex-5 slice can implement an arbitrary logic function of eight variables (Fig. 1). Actually, the successive Shannon expansion (1) of this function by two variables is behind the above structure:

Here, for instance, SOP10  SOP10 (x1,x2,x3,x4,x5,x6) is the Sum-of-Products derived from f(x1,x2,x3,x4,x5,x6,x7,x8) under conditions that x7 = 1 and x8 = 0 as indicated by the lower indices following the SOP-symbol.

II. TWO-STAGE PIPELINE IMPLEMENTATION

The structure shown in Fig. 1 comprises four Xilinx Virtex 5 6-LUTs (one slice) combined with the use of the built-in multiplexers F7 and F8. Since the internal points of the slice are inaccessible for inserting pipeline registers, circuit cannot be pipelined. However, it can be converted into 2 stage pipeline circuit by replacing the built-in multiplexers F7 and F8 with an additional 6-LUT (Fig. 2).

Fig.2. Two-stage pipeline implementation of an arbitrary 8 variable logic function (five 6-LUTs are required)

• At the first stage four SOPs resulting from Shannon expansion are calculated by four 6-LUTs. The results (S1, S2, S3, S4) are latched in the internal registers of the slice.
• At the second stage 6-LUT performs multiplexing by variables x7 and x8.

The 64-bit INIT values for the 6-LUTs, that implement four SOPs, can be retrieved from the function truth table. These four 64-bit strings are in fact the smaller look-up tables resulted from breaking down the original 256-bit look up table.

Compared to the non-pipelined structure (Fig. 1), only one additional 6-LUT is required to perform multiplexing instead of using internal multiplexers F7 and F8. In order for such structure to be generated by the Xilinx Design Tool, it must be specified explicitly (including pipeline registers) with the use of some Xilinx primitives.

Since the internal multiplexers F7 and F8 are not involved, the combinatorial delay at the stages 1 and 2 is determined solely by the delay of 6-LUT. As a result, stage delay of the circuit shown in Fig. 2 is 68 percent less than the circuit shown in Fig. 1.

III. THREE-STAGE PIPELINE IMPLEMENTATION

Because the immediate access to 5-LUT has been retained in Xilinx Virtex-5 FPGA, the more efficient by delay 3-stage pipeline circuit can be built to implement 8-variable logic function (Fig.3). This is possible owing to an additional O5-output. It represents an output of 5-LUT bypassing the built-in multiplexer installed at the output of 6-LUT. That is why the stage delay of this circuit is less than the delay of the circuit containing 6-LUTs at the stage.Xilinx primitive LUT6_2 opens an access to the above possibility [8].

The stage delay of the circuit shown in Fig. 3 is two times less than the delay of the pure look-up table implementation (Fig.1).

• At the first stage eight SOPs of Shannon expansion are calculated by eight 5-LUTs. The results (S₁, S₂, S₃, S₄, S₅, S₆, S₇, S₈) are latched in the registers of the slices.
• At the second stage each of four 5-LUTs performs the selection between two SOPs along with multiplying the result by one of mutually orthogonal products x6 x7, x6 7, 6 x7, 7 6 . The results (P₁, P₂, P₃, P₄) are latched in the internal registers connected to the corresponding 5-LUTs.
• At the third stage 4-variable OR-function is performed. Since the products, mentioned above, are mutually orthogonal, only one of them has a non-zero value and hence OR-function can be used here.

Fig. 3. Three-stage pipeline implementation of an arbitrary 8-variable logic function (thirteen 6-LUTs are required

IV. FOUR-STAGE PIPELINE IMPLEMENTATION IN FRAMEWORK OF XILINX VIRTEX-4

The similar decrease in stage delay can be achieved on condition that Xilinx Virtex-4 series FPGA is selected as target hardware. Since this FPGA has 4 input look-up table as the basic building block, the original 256 bit look-up table of 8-variable logic function can be broken down into sixteen smaller look-up tables. The corresponding 4-stage pipeline circuit is shown in Fig. 4. None of Xilinx Virtex-4 built-in multiplexers is involved. The stage delay of this circuit is solely determined by the delay on the 4-input look-up table (4-LUT). As a result, the stage delay of this circuit is two times less than the delay of a non-pipeline structure where all built-in multiplexers (F5, F6, F7, F8) are in use.

V. CONCLUSION

Some pipeline architectures are proposed for AES S-box implementation on Xilinx Virtex FPGAs. The essence of the approach is that the original truth table of each 8-variable logic function is breaking down into four, eight, or sixteen truth tables as a result of Shannon expansion by two, tree, or four variables. The above small tables fit 6-LUTs, 5-LUTs, or 4-LUTs of Xilinx FPGAs. To select the output of one or another small table, additional LUTs are used instead of internal multiplexers incorporated in the Xilinx slice.

Such transformation allows dividing the circuit into few (two, three, or four) pipeline stages characterized by smaller delay than the delay of the circuit based on the original 256 bit true table as a unit.

Throughput of the AES processor based on the proposed S-box architectures can be 1.5 - 2 times higher than the throughput of the AES processor based on common look-up table S-box.

Some comparison data for Xilinx Virtex-5 and Virtex-4 are shown in Table I.

Although the paper refers to Xilinx FPGA, the similar approach to S-box speeding-up through pipelining is applicable to ASIC look-up table based designs as well. Here, an effect can be even greater thanks to ASIC's fine-grain structure. The best by throughput LUT-based S-box studied in [6] can be made at least two times faster doing nothing but breaking down the initial LUT into set of smaller LUTs in accordance with the suggested approach.

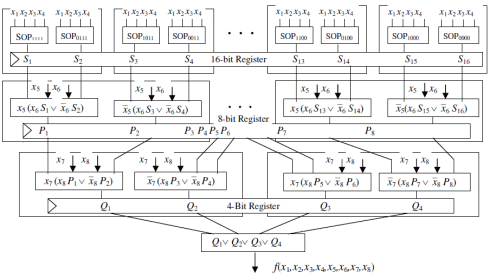
Fig.4. Four-stage pipeline Virtex-4 implementation of an arbitrary 8-variable logic function without internal multiplexers

TABLE I. COMPARISON OF FPGA S-BOX PIPELINE ARCHITECTURES

S-box Architecture (Xilinx Virtex-5, Speed Grade-3)	6-LUTs	Pipeline Registers	Frequency(MHz)	Stage Delay (ns)
Non-pipelined, Fig. 1 (1-stage)	4 x 8 = 32	0	438.673	2.280
2-stage pipeline, Fig. 2	(4 +1) x 8 = 40	4 x 8 + 2* = 34	744.380	1.343
3-stage pipeline, Fig. 3	(8+4+1) x 8 = 104	(8+4) x 8+3* = 99	914.746	1.093
(Xilinx Virtex-4, Speed Grade-12)	4-LUTs
Non-pipelined(1-stage)	16 x 8 = 128	0	425.967	2.348
4-stage pipeline, Fig. 4	(16+8+4) = 224	(16+8+4) x 8+6*=230	860.141	1.163

*) For variables involved into the Shannon expansion to be propagated through a pipeline some extra registers are needed.

In the case of FPGA the benefits of pipelining is substantially reduced owing to:

• high net delay, that is 2-3 times greater than delay caused by logic, and
• the presence of some unavoidable multiplexers that are rigidly incorporated in FPGA.

A. When S-box pipelining may be beneficial

It would be well now to ask what effect can be obtained while pipeline S-box is incorporated into the AES rounds. To gain full advantage from S-Box pipelining the AES rounds have to be fully unrolled. In the case of the partially or fully rolled AES rounds, the gain in the S-box throughput resulted from its pipelining is reduced by unavoidable idle cycles, because the next round cannot be started until the previous one has been finished completely. However in the case of fully rolled AES rounds using 8-bit data path (where only one copy of the S-box is involved) can full advantages are gained from S-box pipelining. In this case, while the last four bytes of the current state (the last column of the state) are still in process, three bytes of the first column of the next state are already accessible for processing by the pipelined S-box. In this way we can avoid any idle cycles on condition that the S-box together with MixColumn has no more than four pipeline stages.

ACKNOWLEDGMENT

The author is grateful beforehand to anyone who will start using this approach in practice and he is ready to join any R&D team to implement the suggested concept in a real hardware.

REFERENCES

[1] "Specification for the Advanced Encryption Standard (AES). Technical Report FIPS PUB 197", (NIST), Nov. 2001, [Online]. Available: http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf.

[2] B. Gladman, "A Specification for Rijndael, the AES Algorithm." [Online]. Abailable: http://fp.gladman.plus.com/cryptography_technology/rijndael/aesspec.pdf.

[3] V. Rijmen, "Efficient implementation of the Rijndael S-box." [Online]. Available: http://www.comms.scitech.susx.ac.uk/fft/crypto/rijndael-sbox.pdf.

[4] S. Morioka and A. Satoh, "A 10 Gbps full-AES crypto design with a twisted-BDD S-box architecture," IEEE Transactions on Vary Large Scale Integration (VLSI) Systems, vol. 12, pp. 689-691, July 2004.

[5] X. Guo, Z. Liu, J. Xing, W. Fan, X. Zou, "Optimized AES crypto desing for wireless sensor networks with balanced S-box architecture," in Proc. Int. Conf. on Informatics and Control Technology (ICT 2006), pp. 203-208.

[6] A. Hodjat and I. Verbauwhede, "Area-throughput trade-offs for fully pipelined 30 to 70 Gbits/s AES processors," IEEE Transactions on Computers, vol. 55, pp. 366-372, Apr. 2006.

[7] "Virtex-5 FPGA User Guide." [Online]. Available: www.xilinx.com/support/documentation/user_guides/ug190.pdf.

[8] "Virtex-5 Library Guide for HDL Design." [Online]. Available: www.xilinx.com/support/documentation/user_guides/ug621.pdf.