By Ealwan Lee (GCT Semiconductor, Inc.)
Abstract :
This paper presents a spatial mapping which turns dual data streams of MIMO system into an equivalent single stream. It is achieved by shrinking the constellation of the secondary stream into that of the primary data stream so that the primary one can be decoded even with a simple SISO de-mapper. Thereby, it can be transmitted through a single antenna and decoded successfully by either a conventional two-antenna MIMO receiver or even a single-antenna receiver. The effective modulation order of the proposed composite stream is the sum of the two data streams resulting in a higher throughput than the maximum of SISO system still conforming to the existing MIMO wireless communication standards.
1. INTRODUCTION
Recent efforts to improve the spectral efficiency of the wireless LAN/MAN communication have been mostly focused on the exploitation of the MIMO channel. Meanwhile, the modulation order has been limited up to 64-QAM in consideration of the implementation issues such as RF impairment and channel fading. The use of MIMO technique, however, requires additional RF transceiver chains and antennas. The increase of material cost, more space and high power consumption was rather off the point to the recently developed small-sized, low-powered personal mobile devices. Ironically, this unleashed the unexpected popularity of the SISO only devices sticking to somewhat aged standard, particularly in WLAN solutions for hand-held devices with a sizable portion in the IoT (Internet-of-Things) connectivity market even today.
If limited to SISO channel, the straightforward way to improve the spectral efficiency of the channel is to simply raise the modulation order. Following this approach, adoption of 256-QAM has been in fashion on reaching the limits of MIMO in recent standardization process [1]. We, however, found out that there remains an alternative way of raising the effective modulation order above 64-QAM with a single antenna still staying in the grammar of old-fashioned standards [2]. The proposed method relies on the nested spatial mapping which merges the dual data paths into a single path [3].
We organized this paper as follows: Section 2 explains the basic idea of adopting nested spatial mapping to the dual MIMO data streams. Then, the constellation ratio between the two streams is optimized for various cases in Section 3. Section 4 gives a numerical evaluation for comparative study followed by the trade-off cases in terms of re-design cost in Section 5 and conclusion in Section 6.
2. NESTED SPATIAL MAPPING
The basic idea of the proposed nested spatial mapping is to shrink the constellation of the secondary data stream at every n-th sub-carrier, s2[n], so that its interference becomes negligible for the primary data stream, s1[n], to be decoded even with a SISO demapper. The power-reduced secondary stream is superposed to the primary one in digital frequency domain with the formula of (1),
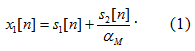
Then, it is transmitted through a single antenna dispensing with the secondary RF chain as shown in Fig. 1. The nesting factor, αM, of 22M-QAM is nominally 2+M to keep the two constellations from overlapping with each other by nesting the constellation of the secondary stream into the primary one completely as disclosed for 16-QAM case in Fig. 2. Since the two data streams share all the subsequent RF chains, they encounter the same propagation channel keeping the power ratio between the two streams constant throughout all the paths and subcarriers.
Cyclic shift diversity (CSD), adopted to prevent unintentional beam forming in MIMO transmission, is not needed in the proposed spatial mapping since all the data streams of this mapping pass only a single physical channel. Besides, CSD rotates the constellation of the secondary stream relative to the primary stream causing the unwanted overlap of the two constellations for the nominal nesting factor of 2+M.
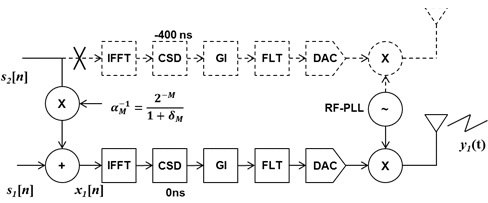
Fig. 1: Block diagram of the nested spatial mapping applied to the 802.11n-compliant dual data MIMO streams.
Since the nested spatial mapping is just a special form of the dual stream transmission through the MIMO channel, most MIMO demappers can be used for the decoding of the received signals without any change. Full-ML equivalent demappers or any kind of successive-interference-cancellation (SIC) demappers like V-BLAST are good choices [4]. It is also well known that a very efficient method of reducing the computational complexity without any sacrifice of the ML performance exists especially in dual data stream cases [5]. However, demappers based on solely a linear de-correlation method such as zero-forcing(ZF) or minimum mean-square error(MMSE) cannot decode this nested MIMO signal as the channel matrix is always ill-conditioned with the rank of 1 ensuing from the use of only a single RF-path in transmission.
Multiple antennas act only as the diversity paths to the proposed MIMO signal in either Tx or Rx. Therefore, even a single antenna reception with conventional full-ML equivalent or SIC demapper is possible for nested MIMO signals with the trade-off of the MRC gain. Among the candidates, an SIC decoder is preferred for its low implementation cost. The decoding performance of SIC demapper is kept comparable with that of full-ML demapper if s1[n] is decoded first in this scheme. Subsequently, the gain of the link throughput above 64-QAM between two single-antenna stations can be obtained with minimal hardware overhead.
3. OPTIMIZATION OF THE NESTING MARGIN
As listed in Fig. 2, the code-word assigned to the 16-levels in an axis (I or Q) for the nested mapping differs from that of the general BICM [6]. The 256-QAM defined in [1] follows the rule of BICM exactly and only a single bit change is found across all the 15 decision boundaries minimizing their hamming distances. However, the proposed spatial mapping encounters two-bit change across the inter-stream boundaries as marked with two thick borderlines in Fig. 2. This discrepancy in the assignment of code-word makes the optimal nesting factor deviate from 6.M dB(=2+M) for 22M-QAM. The BLER as a function of αM illustrated in Fig. 3 shows the optimal nesting factor slightly dislocated from the nominal value of 2+M. This extra nesting factor, nesting margin in short afterwards, δM , defined with
![]()
is approximately below +1 dB minimizing the BLER of 1024-byte packets, Pe, in an AWGN channel with a given SNR for our most meaningful cases of MCS12.
The mathematical estimate of the optimal nesting margin can be derived from the condition of balancing the two probabilities, i.e.
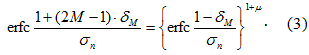
The left hand side accounts for inter-stream bit error coming with two coded bits to be corrected by the channel decoder, thus requiring the 1-bit error probability of intra-stream in the right-hand side to be compensated in exponent for the equivalence between them. To this end, µ has been introduced to explain the effects of the modulation order, channel decoder and punctuation rate as a whole. The typical range of µ is [0 ~ 1]. Using the asymptotic behavior of complementary error function for large input, we could get
![]()
Fig. 2. Constellation of the nested 16-QAM dual-stream signals. 2-bit change across the stream boundary dissimilates the inter-stream and intra-stream bit error probability.
Then, the first order approximation finally yields the simple formula of
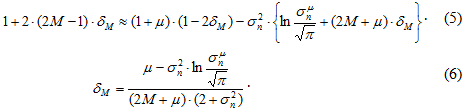
It is noted that ![]() for M=2, i.e. 16-QAM, µ=1 and
for M=2, i.e. 16-QAM, µ=1 and ![]() in good accordance with the nesting margin near 0.9 dB observed in Fig. 3. Here, µ=1 implies that the effect of intra-stream probability on PER becomes equivalent with the inter-stream probability if it is squared. The constraint of small σn is inferred from the fact that the nested MIMO with high MCS will operate in high SNR range above 20dB according to the adaptive modulation and coding (AMC) as in the following simulation result validates the large numbered arguments of erfc(∙) function.
in good accordance with the nesting margin near 0.9 dB observed in Fig. 3. Here, µ=1 implies that the effect of intra-stream probability on PER becomes equivalent with the inter-stream probability if it is squared. The constraint of small σn is inferred from the fact that the nested MIMO with high MCS will operate in high SNR range above 20dB according to the adaptive modulation and coding (AMC) as in the following simulation result validates the large numbered arguments of erfc(∙) function.
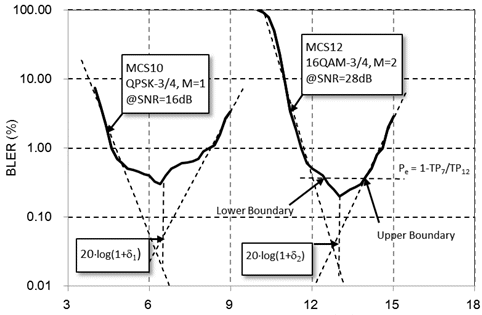
Fig. 3: BLER as a function of the constellation ratio for (QPSK, SNR=16 dB) and (16-QAM, SNR=28dB).
Two asymptotic lines for each PER curves are inter-stream and intra-stream error probabilities where the others can be considered negligible compared to the dominant one. The conditions adopted in (3) leads us to locate the cross points of these two lines near the optimal point of simulation results.
The nesting margin should be distinguished from the constellation ratio or injection level often referred in hierarchical modulation widely suggested in broadcasting technology [7][8][9]. The constellation factor in hierarchical modulation has been introduced mainly for the unequal error protection of two independent data streams simply as a means of trade-off between twos while nesting margin of this paper is required for the minimization of overall BLER. Above all, the composite constellation of the hierarchical mapping of [7][8] follows the code assignment of BICM by making the secondary stream the function of the first stream. However, the proposed one cannot in order to stay in the grammars of the pre-existing standard as already stated.
4. NUMERICAL RESULTS
Quantitative property of the nested spatial mapping has been evaluated by measuring the throughput of the 802.11n WLAN as an example. Channel estimation per subcarrier was enforced by clearing the smoothing bit field of HT-SIG to indicate a beam forming not actually used but alleging its use in neutralizing the effect of CSD for rigorous compliance to the standard [2]. It is reminded that the time domain shift can be simulated with the sub-carrier dependent frequency domain rotation matrices in the form of beam forming. The maximum throughput of HT20 (20MHz channel band-width 802.11n packet) with MCS7 (a single stream, 64-QAM, 5/6- code rate and short-guard-interval) is 72.2Mbps. The nested MIMO signal with MCS12 (two streams, 16-QAM , 3/4-code rate) achieves 86.7Mbps, 20% gain in link throughput, as shown in Fig. 4.
The curve of the optimal nesting factor plotted over the graph in Fig. 4 exhibits its low sensitivity against the SNR staying near 13 dB with no significant variation in throughput. It is quite well explained by (6) typically in the range of σn≪1, which serves as a useful property to simplify the optimization process in practical application.
The range of the nesting margin can be defined where the throughput of MCS12 with the nested spatial mapping, TP12, is above the max throughput of conventional single stream MCS7, TP7. We also know that the throughput of the ARQ-based system is proportional to corresponding BLER. Thus, BLER below (1 - TP7/TP12) can be used for the confidence level of the optimal nesting margin as marked in Fig. 3. Its wide range clearly observable as the plateau in Fig. 4 re-affirms the validity of the formula (6).
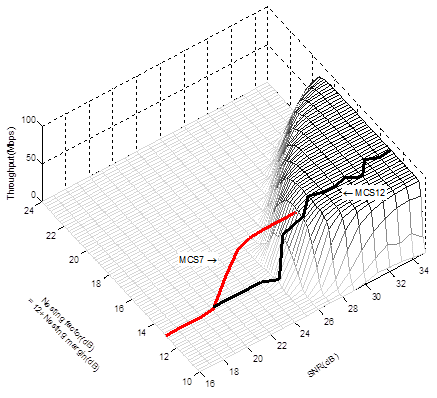
Fig. 4.: Throughput of the nested MIMO 16-QAM(MCS12) versus the 802.11n 64-QAM(MCS7) over the range of SNR and nesting factor. Optimal nesting factor is also plotted as a function of SNR.
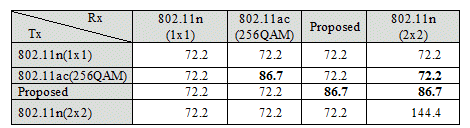
Table 1. Peak throughput allowed for each link of HT20/802.11n and VHT20/802.11ac. The main difference lies in the link of HT20 with 2x2 capabilities.
5. EXAMPLES OF APPLICATION : TRADE-OFF IN TERMS OF RE-DESIGN COST
As stated in the introduction, the proposed method is for the full utilization of the already built/purchased MIMO IPs for both IP vendors and the customers. IP vendors may want to diversify their IP line-ups with a minimal development cost. Customers, who have already purchased MIMO IP from some IP vendors, may try to re-use their assets with minimal cost of re-design if possible and there are some points that can be trade-off to their goals.
5.1. PHY HARDWARE SIDE
In either case of IP vendors or customers, a simple programmable ratio combiner outside of the box in time-domain before the input of Tx DAC, rather than in the frequency domain, can be a good choice in minimizing the re-design cost, although Section 2 suggested the optimal point in terms of silicon area. However, setting the CSD of the secondary path, mostly programmable, is still recommended not to suffer from unwanted SNR loss. It still holds that only a single RF path and Tx DAC is required.
The second point is the trade-off between the maximum throughput target and re-design cost. As figured out in Section 4, the throughput gain achieved with the proposed method is 20%, which soars above the throughput limit of already designed IP, 80Mbps of the Viterbi decoder of radix-2 operating at 80 MHz or of radix-4 operating at 40 MHz from the typical configuration. In this case, use of only 800ns (long) guard interval assures the minimal change of the receiver design though the throughput gain is lowered from 20%(86.7 Mbps) to 8%(78 Mbps). Although we have focused only on HT20 in this paper, a simple extension is also possible to HT40, i.e. from 150 Mbps to 180 Mbps.
Existing ML decoder, replacing the area-efficient SIC decoder proposed only for nested spatial mapping, can still be used simply trimming the implementation option to support only up to 16-QAM if allowed. The computational complexity is significantly reduced by 75% from 128 ML candidates to 32 ML candidates as the computational complexity of dual stream MIMO ML decode is O(2∙M)[5].
5.2. MAC SOFTWARE SIDE
Accordingly, however, a minimum modification of MAC firmware is inevitable to announce the dual data stream TX capabilities of the re-designed IP by setting <99:98> of Supported MCS set field in HT Capabilities element. The RX capability, however, in a single antenna is strictly restricted so that turning on the capabilities of MCS8~12 induces a confusion to the network. Instead, the increase of Rx Highest Supported Data Rate at <89:80> of Supported MCS set field in HT Capabilities element can be used to hint its RX capability [2]. Most other STA or APS ignore the data rate larger than the number derived from the MCS, but the IPs with the proposed method detects the counter part is the same kind as themselves.
It may be argued that adoption of a 256-QAM feature in 802.11ac makes all the business clear and simple. However, although 802.11ac now permits the single antenna operation unlike 802.11n enforced with two receiver path and more, it enforces 80 MHz band-width operation to differentiate from the olds [1]. This formidable mandatory feature inhibits the 256-QAM technology from being used to simply boost the legacy link especially in 2.4 GHz ISM band requiring fast thus expensive ADC, DAC and wide RF path. On the contrary, the proposed nested spatial mapping does not impose any obligation if they simply start from HT20 802.11n dual stream IP but still staying in the grammars of standards without breaking any rule as exemplified in Table 1.
6. CONCLUSION
A simple but effective method of raising the modulation order to improve the spectral efficiency by transmitting a dual-stream with a nested spatial mapping has been proposed. An example with dual 16-QAM streams of 802.11n presents that it can be transformed into a 256-QAM equivalent single stream resulting in the gain of throughput by 20% compared with 64-QAM single stream. Furthermore, the nesting factor for optimal performance owns a good property of being rather insensitive to the channel condition such as CSI. Above all, the proposed mapping keeps the stream compliant to the dual data stream format defined in most currently existing wireless communication standard specification and allows the legacy two-antenna systems receive it seamlessly. Thereby, already developed MIMO WLAN IPs can get another chance for a cost-sensitive single antenna application mostly required in today’s diverse areas of IoT connectivity market with an increased throughput if needed.
REFERENCES
[1] IEEE, “IEEE P802.11ac - Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) specifications, Amendment 4: Enhancements for Very High Throughput for Operation in Bands below 6 GHz”, Dec 2013.
[2] IEEE, “IEEE Std802.11 - Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) specifications”, Feb 2012.
[3] E. Lee, D. Kim and J. Kim, “Transmission method for dual digital signal through single antenna, transmitter for dual digital signal through single antenna and receiving method for dual digital signal through single antenna”, U.S. Patent 9 014 289, issued April 21, 2015.
[4] G. D. Golden, C. J. Foschini, R. A. Valenzuela and P. W. Wolniansky, “Detection algorithm and initial laboratory results using V-BLAST space-time communication architecture”, Electronics Letters, vol. 35, no. 1, pp. 14-16, Jan 1999.
[5] Y.Lomnitz and D Andelman, “Efficient maximum likelihood detector for MIMO systems with small number of streams”, Electronics Letters, vol. 43, no. 22, Oct 2007.
[6] G. Caire, G. Taricco and E. Biglieri, “Bit-Interleaved Coded Modulation”, IEEE Trans. Inf. Theory, vol. 44, no. 3, pp. 927-946, May 1998.
[7] A. Shertz and C. Weck, “Hierarchical modulation - the transmission of two independent DVB-T multiplexes on a single frequency”, EBU Techn. Rev., Apr 2003.
[8] H. Jiang and P. Wilford, “A hierarchical modulation for upgrading digital broadcast systems”, IEEE Transactions on broadcasting, vol. 51, no. 2, pp. 223-229, Jun 2005.
[9] S. I. Park et al., “Low complexity layered division multiplexing for ATSC 3.0”, IEEE Transactions on broadcasting, vol. 62, no. 1, pp. 233-243, Mar 2016.
