Specifying a PLL Part 1: Calculating PLL Clock Spur Requirements from ADC or DAC SFDR

By Julian Jenkins, Perceptia Devices

Introduction

It is common for an ADC or DAC to be required to meet a SFDR (spurious free dynamic range) specification.

Definition:

“Spurious-free dynamic range (SFDR) is the strength ratio of the fundamental signal to the strongest spurious signal in the output. It is also defined as a measure used to specify analog-to-digital and digital-to-analog converters (ADCs and DACs, respectively) and radio receivers.”

Or in simpler terms, it is the ratio between the power of the strongest unwanted tone in the output and the desired signal.

In high end RF systems, such as 5G radios, the requirements are so stringent that the source of this strongest unwanted tone can be the PLL. This article outlines how spurs in the input clock to the ADC or DAC may limit the SFDR. This in turn will set the requirements for the spurs for the input clock (from a PLL), in order to achieve a specific SFDR.

Theory

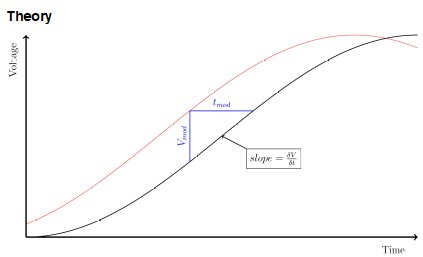
Figure 1: The slope of a curve

If we consider the time at which a signal passes through a threshold, we can see that modulation in the time and voltage domains can be considered equivalent. Figure 1 shows us the translation, adding time modulation of t_mod to a signal, shifts the signal by V_mod in the voltage domain.

Consider the operation of a DAC, generating the black output signal shown in Figure 1. If the sampling times at which the DAC outputs are varied by an amount t_mod, indicated by the horizontal blue line, the output would be shifted to become the red signal. At the instant in time indicated by the vertical blue line, the voltage output by the DAC differs by V_mod between these two signals.

If we apply a time varying modulation of the sampling times of the DAC (otherwise known as jitter) with amplitude t_mod, the resulting output of the DAC will be equivalent to a signal with modulation amplitude V_mod.

Note that the modulation in Figure 1 is strongly exaggerated in Figure 1 to make it easy to see. The mathematics below only apply to small signal modulation. Luckily, when using an RF quality PLL, such as Perceptia’s pPLL08, all such unwanted modulation will very small and the calculations can be trusted.

The equivalent analysis applies to an ADC. Varying the sampling time of the ADC, will similarly change the voltage observed at the sampling instant, resulting in a different output code. The mathematics below apply equally to DACs and ADCs, despite only being described for the case of the DAC.

While the description above, related this to the sampling of an ADC or DAC, the mathematics apply more generally to any signal. The remainder of this article will describe this for the DAC, but the mathematics apply equally well to the ADC or other similar cases.

Putting this into mathematical terms that support analysis, we can see that the relationship between V_mod and t_mod is determined by the slope of the signal:

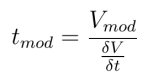
In particular, this applies to how voltage modulation changes the time when a signal consisting of a single tone passes through a threshold. This allow us use the slopes of the clock and output to predict that the modulation in the sampling clock (V_{ck_mod}) to an DAC will modulate the output signal (V_{out_mod}) as follows:

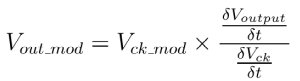
When measuring SFDR we are typically looking for individual tones, the spurs, that exceed the noise floor of the DAC. This means that we can complete the analysis for the case of sinusoidal signals. For a sine wave, the maximum slope of the signal is proportional to the frequency(f_sig) and amplitude(V_sig) of that signal.

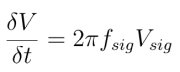
Applying this to the equations above, we can rewrite our expression for the modulation on the output signal, after canceling out the factors of 2 π as:

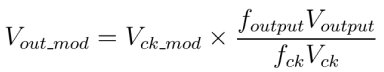
We can rearrange this to get an expression for the relationship between the modulation on the output signal and of the DAC or DAC the modulation on its sampling clock:

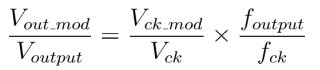
Interestingly, this equation tells us that the modulation in the output is reduced by the ratio between the sampling clock and the output frequency. This makes sense because a lower output frequency is going to result in a lower slope.

The SFDR is typically specified in dB. This aligns well with typical practice, where we will measure all the voltage parameters in this equation using the spectrum analyzer. Defining SFDR in dB, we get:

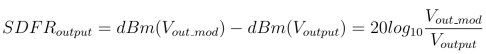
That is the SFDR of the output signal, SFDR_output, is 20log₁₀ of the ratio between the amplitudes of the modulation and the output. This is measured by subtracting the power of the output tone from the power of the modulation signal, both measured in dBm by the spectrum analyzer. Remember that the difference between two measurements in dBm is a ratio in dB.

The measurement of an ADC is more complicated. The SFDR must be calculated using a DFT (discrete Fourier transform) or equivalent to determine the ratio between the amplitudes of these two components in the digital domain.

We can define a similar relationship for the clock signal:

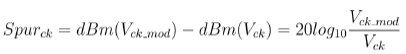
The PLL Spur Requirement

When we convert our relationship equation from above into dB, by taking 20log₁₀ of both sides of the equation and substituting, we get:

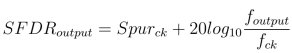
This equation tells us that the SFDR of the output of the ADC or DAC is the power of the largest clock spur reduced by the ratio between the clock frequency and the largest tone in the output signal. This is the key relationship that we were looking for.

We can rearrange this equation give us an expression for the maximum allowable spur on the output of the PLL in order to achieve a given SFDR at the output of a DAC or ADC:

Example

A notional 5G base station, the ouput of the DAC that drives the transmitter mixer can have 350MHz of bandwidth. This DAC can have an SNDR requirement of -60dB. The ADC receiving the signal from the receiver mixer can have similar specifications.

It is common for the DAC in such a system to sample at 1966.08MHz. Hence, for the highest frequency component of the signal, within the DAC’s bandwidth, the component of the equation above related to the ratio of frequencies becomes:

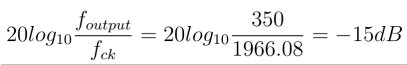
From above, the requirement was that SFDR_output = -60dB. So the equation for this becomes:

And we can see that the maximum spur allowed on the sampling clock of the DAC, Spur_ck is -45dB.

Perceptia’s pPLL08 is designed with this requirement in mind and has no spurs exceeding -45dB, measured from a 1966.08MHz carrier. This is a critical specification for many RF systems.

Experienced ADC designers will know that this is not the only driver of SFDR and that all other sources must also be optimized to meet the requirement.

Conclusion

SFDR is an important parameter when specifying a DAC or ADC and its support circuitry for an RF system. This article gives the basic mathematics required to calculate the requirements of the input clock and specify the PLL needed to support those requirements.

SFDR is an important spec for DACs and ADCs used in RF systems and many other applications. It is critical that you ensure that the PLL you choose for your system has sufficiently low spurs to support the SFDR required by your system. The team at Perceptia has designed pPLL08 specifically to address the requirements of RF systems such as 5G and 802.11ax WiFi. pPLL08 has jitter less than 300fs and spurs below -45dB on a 1966.08MHz carrier in order to support these requirements.

About the Author

Julian Jenkins, is the CEO and CTO of Perceptia Devices. As CTO, he is the architect of all of Perceptia’s PLL IP where he been among the pioneers in the development of all digital PLLs. Julian has several US and international patents as a result of this work. He has participated in an impressive list of high-speed analog and mixed-signal ICs that are in commercial production. Feel free to contact Julian if you have questions about this topic.

Perceptia Devices is an IP and design services provider, based in Sydney, Australia and Silicon Valley. It is focused on PLLs for RF systems and demanding clocking applications.

References

If you wish to download a copy of this white paper, click here